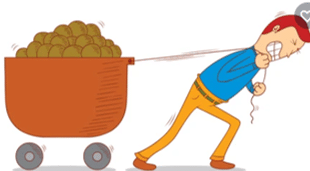
Definition of work in physics: The work done on a system by a constant force is the product of the force component in the direction of motion multiplied by the distance over which the force acts.
For one-way motion in one dimension, the work formula is given as W = Fd cos θ, where W is work, F is the magnitude of the force on the system, d is the magnitude of the displacement of the system, and θ is the angle between the force vector F and the displacement vector d.
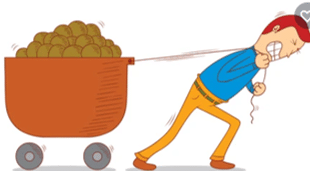
Table of Contents
Daily Life Simple Examples of Work
Some examples of work done are listed below:
- Lifting an object: Lifting an object involves doing labor on it. The labor done is equal to the force used to lift the object multiplied by the distance traveled.
- Pushing a car: When you push an automobile, you exert a force across a long distance, which suggests you are working. The labor done is equal to the force used to push the car multiplied by the distance pushed.
- Digging a hole: When you dig a hole, you use force to move dirt, which means you are working. The work done is equal to the force used to move the dirt multiplied by the distance moved.
- A person pushing a grocery cart in a shopping mall
- A hand applies a force on the ball over this distance while throwing a ball; the hand is doing work on the ball, and the ball gains kinetic energy.
- a weightlifter lifting a barbell above his head.
- When a ball is thrown upwards, the force produces positive work.
Work Formula and Unit
The basic SI unit of work is the joule (symbol: J). A joule is the kinetic energy of a kilogram mass moving at the velocity of one meter per second (one joule equals a kg.m2/sec2). It is also the amount of work done on an object when a force of one newton acts in the direction of the object’s motion over a one-meter distance (1 joule equals 1 newton meter or Nm). The unit bears the name of James Prescott Joule.
Joule
The unit of work is the joule. one Joule is the amount of work done when a force of 1 Newton is applied over a distance of 1 meter.
Joule = N.m
Joule= kg.m2/sec2
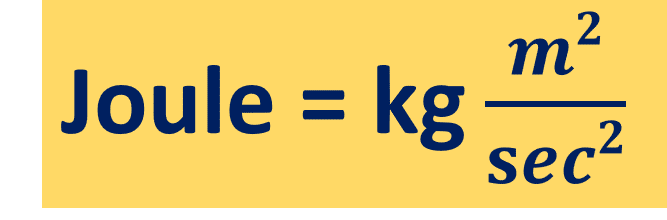
Can Work Be Negative?
Work is done when a force acting on a body displaces it in the direction of a force. For instance, the work done by a moving object equals 1 Joule when a force of 1 Newton is applied over 1 meter of distance. Since the applied force can be negative or positive, therefore, work can be negative or positive.
The motion of a body against the force of friction is an example of negative work.
Negative work occurs when a force acts in the opposite direction of the motion of an object, effectively reducing the amount of work being done. Here are a few examples of negative work:
- Lowering an object: When you lower an object, you are applying a force in the opposite direction of the motion of the object, which means you are doing negative work. The work done is equal to the force you apply to lower the object, multiplied by the distance over which you lower it.
- Slowing down a moving object: When you slow down a moving object, you are applying a force in the opposite direction of its motion, which means you are doing negative work. The work done is equal to the force you apply to slow down the object, multiplied by the distance over which it moves while being slowed down.
- Stopping a spinning wheel: When you stop a spinning wheel, you are applying a force in the opposite direction of its rotation, which means you are doing negative work. The work done is equal to the force you apply to stop the wheel, multiplied by the distance over which it rotates while being stopped.
In all these examples, negative work is being done to reduce the energy of the system. The more force you apply and the greater the distance over which it is applied, the more negative work you do.
Commonly used Formulas related to Work
| No. | Formula | Description | Daily Life Example |
|---|---|---|---|
| 1 | Work = Force x Distance | The amount of work done by a force over a certain distance | Lifting a weight off the ground |
| 2 | Work = Force x Displacement x cos(θ) | The amount of work done by a force over a certain displacement at an angle θ | Pushing a lawnmower up a hill |
| 3 | Work = Pressure x Area x Distance | The amount of work done by a fluid under pressure over a certain distance | Water flowing through a turbine |
| 4 | Work = Power x Time | The amount of work done over a certain period of time, where power is the rate at which work is done | Running a 5k race |
| 5 | Power = Work / Time | The rate at which work is done over a certain period of time | Riding a bike up a hill at a steady pace |
| 6 | Potential Energy = mgh | The amount of potential energy an object has due to its height above a reference point, where m is the mass of the object, g is the acceleration due to gravity, and h is the height | A roller coaster at the top of a hill |
| 7 | Kinetic Energy = 1/2 mv^2 | The amount of kinetic energy an object has due to its motion, where m is the mass of the object and v is its velocity | A ball rolling down a hill |
| 8 | Work-Energy Principle: Work = Change in Kinetic Energy | The principle that the work done on an object equals its change in kinetic energy | A baseball player hitting a home run |
Common Units used to measure Work
| No. | Unit | Symbol | Description | Daily Life Example |
|---|---|---|---|---|
| 1 | Joule | J | The standard unit of work and energy in the International System of Units (SI), is defined as the amount of work done by a force of one newton over a distance of one meter. | Lifting a 1kg weight 1 meter using a force of 1 newton |
| 2 | Newton-meter | N·m | An alternate unit of work, equal to one joule. | Tightening a bolt with a torque wrench |
| 3 | Foot-pound | ft·lb | A unit of work commonly used in the United States and other countries that measures the work done by a force of one pound over a distance of one foot. One foot-pound is approximately 1.3558 joules. | Turning a wrench to loosen a bolt |
| 4 | Calorie | cal | A unit of energy commonly used in nutrition that measures the amount of energy required to raise the temperature of one gram of water by one degree Celsius. One calorie is approximately 4.184 joules. | Burning calories during exercise |
| 5 | Kilowatt-hour | kWh | A unit of energy commonly used to measure electrical energy consumption, equal to one kilowatt of power used for one hour. One kilowatt-hour is equal to 3,600,000 joules. | Paying for electricity usage on a monthly bill |
Work-Energy Theorem
The work done by the total of all forces acting on an item equals the change in kinetic energy of the object, according to the work-energy theorem (or), the net work done on a system equals the change in kinetic energy. For details, please check the article “Work energy theorem”.
Summary
- The work done on a system is defined as the product of the force component in the direction of motion multiplied by the distance over which the force acts.
- The basic SI unit of energy is the joule (symbol: J).
- A joule is the kinetic energy of a kilogram mass moving at the velocity of one meter per second (one joule equals a kg.m2/sec2).
More Links
Work-Formula, Definition, & Units
Mechanical Energy Formula & Examples
Kinetic Energy Formula
Light Energy| Definition, and Properties
Stress in Physics| Definition and Easy Examples
Electromagnetic Force- An Overview
- BCl3 Lewis Structure in four simple steps - November 1, 2023
- PH3 Lewis Structure in four simple steps - October 8, 2023
- PF3 Lewis structure in four simple steps - September 24, 2023